Matrix Calculus for DeepLearning (Part2)
May 29, 2020

We can’t compute partial derivatives of very complicated functions using just the basic matrix calculus rules we’ve seen Blog part 1. For example, we can’t take the derivative of nested expressions like sum(w + x) directly without reducing it to its scalar equivalent. We need to be able to combine our basic vector rules using the vector chain rule.
In paper they have defined and named three different chain rules.
- single-variable chain rule
- single-variable total-derivative chain rule
- vector chain rule
The chain rule comes into play when we need the derivative of an expression composed of nested subexpressions. Chain rule helps in solving problem by breaking complicated expressions into subexpression whose derivatives are easy to compute.
Single-variable chain rule
Chain rules are defined in terms of nested functions such as y=f(g(x)) for single variable chain rule.
Formula is
dy/dx = (dy/du) (du/dx)
There are 4 steps to solve using single variable chain rule
- Introduce intermediate variable
- compute derivatives of intermediate variables wrt(with respect to) their parameters.
- combine all derivatives by multiplying them together
- substitute intermediate variables back in derivative equation.
Lets see example of nested equation y = f (x) = ln(sin(x³ ) ² )

It is to compute the derivatives of the intermediate variables in isolation!
But single variable chain rule is applicable only when a single variable can influence output in only one way. As we see in example we can handle nested expression of single variable x using this chain ruleonly when x can effect y through single data flow path.
Single-variable total-derivative chain rule
If we apply single variable chain rule to y = f (x) = x + x² we get wrong answer, because derivative operator doesnot apply to multivariate functions. change in x in the equation , affects y both as operand og addition and as operand of square. so we clearly cant apply single variable chain rule. so…
we move to total derivatives.
which is to compute (dy/dx) , we need to sum up all possible contributions from changes in x to the change in y.
Formula for total derivative chain rule
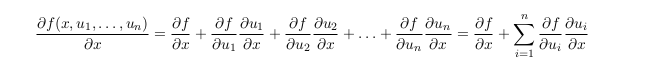
Total derivative assumes all variables are potentially co-dependent where as partial derivative assumes all variables but x are constants.
when you take the total derivative with respect to x, other variables might also be functions of x so add in their contributions as well. The left side of the equation looks like a typical partial derivative but the right-hand side is actually the total derivative.
Lets see example,
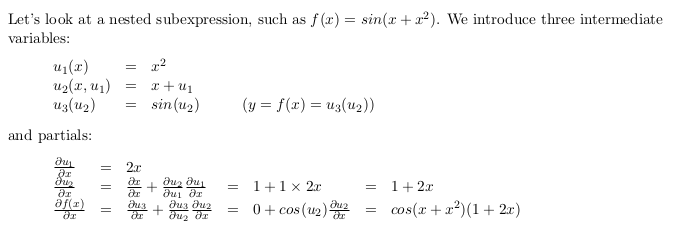
total derivative formula always sums, that is sums up terms in the derivative. For example, given y = x × x² instead of y = x + x² , the total-derivative chain rule formula still adds partial derivative terms, for more detail see demonstration in paper.
Formula of total derivative can be simplified further.

This chain rule that takes into consideration the total derivative degenerates to the single-variable chain rule when all intermediate variables are functions of a single variable.
Vector chain rule
derivative of a sample vector function with respect to a scalar, y = f (x).

introduce two intermediate variables, g 1 and g 2 , one for each f i so that y looks more like y = f (g(x))

If we split the terms, isolating the terms into a vector, we get a matrix by vector.

The vector chain rule is the general form as it degenerates to the others. When f is a function of a single variable x and all intermediate variables u are functions of a single variable, the single-variable chain rule applies. When some or all of the intermediate variables are functions of multiple variables, the single-variable total-derivative chain rule applies. In all other cases, the vector chain rule applies
This completes chain rule. In next blog that is part3 we will see how we can apply this gradient of neural activation and loss function and wrap up.
Thank you.
Useful Points:
It is difficult while writing blog in markdown to convert to superscript and subscript so I have listed down , which you can use ( copy paste) in your markdown
super script ⁰ ¹ ² ³ ⁴ ⁵ ⁶ ⁷ ⁸ ⁹ ᵃ ᵇ ᶜ ᵈ ᵉ ᶠ ᵍ ʰ ᶦ ʲ ᵏ ˡ ᵐ ⁿ ᵒ ᵖ ʳ ˢ ᵗ ᵘ ᵛ ʷ ˣ ʸ ᶻ
subscript ₀ ₁ ₂ ₃ ₄ ₅ ₆ ₇ ₈ ₉ ₐ ᵦ 𝒸 𝒹 ₑ 𝒻 𝓰 ₕ ᵢ ⱼ ₖ ₗ ₘ ₙ ₒ ₚ ᵩ ᵣ ₛ ₜ ᵤ ᵥ 𝓌 ₓ ᵧ 𝓏
# Blog 10