Matrix Calculus for DeepLearning (Part1)
May 29, 2020

Credits: Based on Paper The Matrix Calculus You Need For Deep Learning by Terence Parr and Jeremy Howard. Thanks for this paper.
The paper is beginner-friendly, but I wanted to write this blog to note down points which would make it easier to understand the paper much better. As we learn some topics which are slightly difficult, we find it to explain to a beginner, in a way we learnt, who may not know anything in that field, so this blog is for beginner.
Deep Learning is all about linear algebra and calculus. If you try to read any deep learning paper, matrics calculus is a needed component to understanding the concept. May be word need may not be the right word to use, since Jeremy’s courses show how to become a world-class deep learning practitioner with only a minimal level of calculus,\ check fast.ai for courses.
I have written my understanding of paper in form of three blogs. This is part1 and check this website for two more parts.
Deep learning is the basically use of neurons with many layers. what does each neuron do??
Introduction
Each neuron applies a function on input and gives an output. The activation of a single computation unit in a neural network is typically calculated using the dot product of an edge weight vector w with an input vector x plus a scalar bias (threshold):
z(x) = w · x + b
letters written bold are vectors. w is vector
Function z(x) is called the unit’s affine function and is followed by a rectified linear unit, which clips negative values to zero: max(0, z(x)). This computation takes place in neurons. Neural networks consist of many of these units, organized into multiple collections of neurons called layers. The activation of one layer’s units becomes the input to the next layer’s units. Math becomes simple when inputs, weights, and functions are treated as vectors, and the flow of values can be treated as matrix operations.
The most important math used here is differentiation, calculating the rate of change and optimizing the loss function to decrease error is the main purpose. Training phase is all about choosing weights w and bias b so that we get the desired output for all N inputs x. To do that, we minimize a loss function. To minimize the loss, we use SGD. Measuring how the output changes with respect to a change in weight is the same as calculating the (partial) derivative of the output w.r.t weight w. All of those require the partial derivative (the gradient) of activation(x) with respect to the model parameters w and b. Our goal is to gradually tweak w and b so that the overall loss function keeps getting smaller across all x inputs.
Scalar derivative rules
Basic rules needed during to solve problem

Partial derivatives
Neural networks are functions of multiple parameters so let’s discuss that.\ What is derivative of xy(multiply x and y) ??\ Well, it depends on whether we are changing with respect to x or y. we compute derivatives with respect to one variable at a time, giving two derivates in this case, we call partial derivatives. δ symbol is used instead of d to represent that.\ The partial derivative with respect to x is just the usual scalar derivative, simply treating any other variable in the equation as a constant.
Matrix calculus
we will see how to calculate the gradient of f(x,y)

The gradient of f(x,y) is simply a vector of its partials.\ Gradient vectors organize all of the partial derivatives for a specific scalar function. If we have two functions, we can also organize their gradients into a matrix by stacking the gradients. When we do so, we get the Jacobian matrix where the gradients are rows.
To define the Jacobian matrix more generally, let’s combine multiple parameters into a single vector argument: f (x, y, z) ⇒ f (x)
Let y = f (x) be a vector of m scalar-valued functions that each take a vector x\ of length n = |x| where |x| is the cardinality (count) of elements in x. Each f of i is a function within f returns a scalar\ for example f (x, y) = 3x²y and g(x, y) = 2x + y⁸ from the last section as
y₁ = f₁(x) = 3x²₁x₂
y₂ = f₂(x) = 2x₁ + x⁸₂
Jacobian matrix is the collection of all m × n possible partial derivatives (m rows and n columns), which is the stack of m gradients with respect to x.
The Jacobian of the identity function f(x) = x, with fi (x) = x i , has n functions and each function has n parameters held in a single vector x. The Jacobian is, therefore, a square matrix since m = n
Element-wise operations on vectors
Element wise operations are important to know in deep learning. By Element-wise binary operations we simply mean applying an operator to the first item of each vector to get the first item of the output, then to the second items of the inputs for the second item of the output, and so forth. We can generalize the element-wise binary operations with notation y = f (w) O g(x) where m = n = |y| = |w| = |x|

Derivatives involving scalar expansion
When we multiply or add scalars to vectors, we’re implicitly expanding the scalar to a vector and then performing an element-wise binary operation. For example
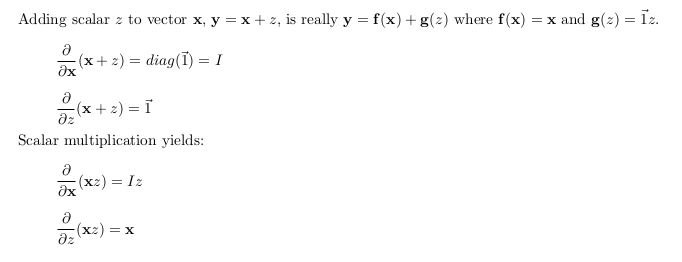
(The notation -> 1 represents a vector of ones of appropriate length.) z is any scalar that doesn’t depend on x, which is useful because then ∂z/∂x= 0 for any x i and that will simplify our partial derivative computations
Vector sum reduction
Summing up the elements of a vector is an important operation in deep learning, such as the network loss function.\ Let y = sum(f (x)) . Notice we were careful here to leave the parameter as a vector x because each function f i could use all values in the vector, not just x i . The sum is over the results of the function and not the parameter.

In gradient of the simple y = sum(x)= [1,1 …1]. Because ∂x i/ ∂x j = 0 for j != i. Transpose because we have assumed default as vertical vectors. It’s very important to keep the shape of all of your vectors and matrices in order otherwise it’s impossible to compute the derivatives of complex functions.
#Blog 9
Links that helped me: Paper The Matrix Calculus You Need For Deep Learning by Terence Parr and Jeremy Howard.\ Blog by Nikhil B
This is part 1 of the blog, In blog 2, I will explain chain rule.